Mathematics

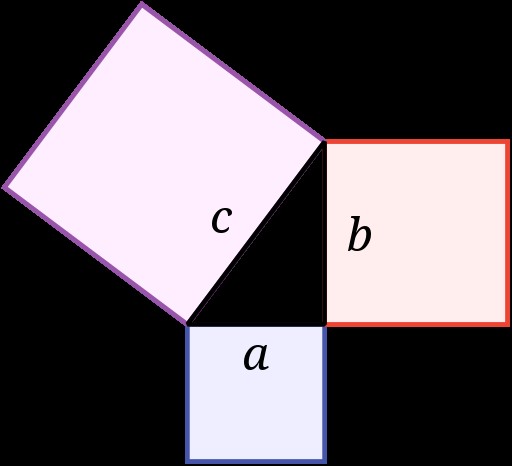
Geometry

Geometry studies figures, especially with regard to their rigid properties, and as a deductive science it began, like mathematics itself, with the Greeks. Straight lines, triangles, circles, spheres and cubes are among the first figures studied. A typical theorem, or general statement arrived at deductively, is that a right-angled triangle is characterized by the Pythagorean property (e.g., the square of the hypotenuse is equal to the sum of the squares of the other two sides).

In the early period (600 BCE - 100 CE), the theory of conic sections (ellipses, hyperbolas, parabolas) was developed, as was trigonometry, important for astronomy. In addition, formulas for the area or volume of special figures were discovered and proved. The principal later developments were the introduction of co-ordinate geometry (Descartes) and of curvature (Gauss), the central notion of differential geometry. The discovery of non-Euclidean geometry is, in comparison, minor.

In co-ordinate geometry the points of a plane are labelled by two co-ordinates, its distances from the two axes, and familiar figures become the loci of points satisfying an algebraic equation. Thus, geometry is incorporated into algebra and the way is opened for the introduction of spaces of arbitrarily large dimension, important in mechanics. Curvature, in its simplest form, is a number attached to a surface at a point. The flatter the surface, the smaller the number (positive for a sphere, negative for a saddle-shaped surface).

Topology

Topology studies properties of figures or spaces that are invariant under deformation. It has had its greatest successes in higher dimensions and studies spaces by attaching algebraic and numerical invariants to them. For example, closed oriented surfaces are characterized by their genus. For the surface of a ball, g = zero; of a doughnut, g = one; and of a pretzel, g = two. The classification of three-dimensional spaces, of much current interest, is still incomplete. The Gauss-Bonnet theorem connects topology and geometry in a typical way: the integral of the curvature over a closed surface equals four Pi (one-g).

Algebra

Algebra studies general properties of the solutions of one or several equations; arithmetic or number theory is the study of solutions in specific domains or fields of numbers: e.g., solutions of xn + yn= zn in whole numbers as in Fermat's theorem. Linear algebra, the highly developed theory of equations of degree one, is of importance throughout mathematics. The notion of eigenvalues and eigenvectors, which appear geometrically as the principal axes of an ellipsoid, is critical. All of algebra is pervaded by the concept of a group, a collection of elements which can be multiplied, such as operations on a Rubik's cube. The theory of finite groups has made great strides in recent years.

Analysis

Analysis begins with calculus, the calculation of velocities and tangents (derivatives), lengths, areas and distances traversed (integrals), and maxima and minima. The central notion is that of a function, which expresses the way one variable depends upon another. The integrals of very few functions can be calculated explicitly; the attendant problems for algebraic functions have greatly influenced the development of geometry and arithmetic.

A differential equation is one connecting a function and its derivatives. Differential equations arise in all sciences. The equation is ordinary if there is only one independent variable and two of the basic problems are stability and the existence of periodic solutions. Much is known but the empirical data, found by computer, outstrip our theoretical understanding.

The equation is called partial if there is more than one independent variable. Partial differential equations appear in the study of the propagation of waves and matter. In spite of an enormous theory, there are still basic phenomena that we do not understand, such as turbulence, and to which ideas from probability, a discipline in its own right, are often applied. Derivatives and integrals require the use of limits, as do expansions of functions in infinite series, such as a power series or Fourier series. The use of Fourier series, which express a function as an infinite sum of sines and cosines, is indispensable in the study of partial differential equations.